Legea lui Benford si datele Eurostat despre silvicultura
In ultimele luni, odata cu aparitia datelor despre infectarile cu COVID-19, s-a vorbit destul de mult pe diverse platforme despre legea lui Benford sau legea primei cifre asa cum mai este numita. Aceasta lege, care de fapt nu este a lui Benford, fiind descrisa pentru prima data de Simon Newcomb in 1881 [1], dar care poarta numele lui Frank Benford datorita lucrarii acestuia din anul 1938, numita Legea Numerelor Anormale [2], este foarte des folosita pentru detectarea datelor frauduloase, adica a datelor fabricate sau masluite.
Lege spune ca intr-un sir de numere, distributia frecventelor primei cifre nu este uniforma (fiecare cifra apare cu o probabilitate egala de 11%) ci negativ exponentiala. Practic, 30.1% din numerele sirului vor incepe cu cifra 1 pe cand doar 4.6% vor incepe cu cifra 9. Tot Benford in lucrarea lui propune urmatoarea relatie logaritmica pentru a determina frecventa primelor cifre in distributie: $$ F_a= log(\frac{a+1}{a}) $$ unde $F_a$ reprezinta frecventa cifrei $a$ ca prima cifra a unui numar iar $log$ este in baza 10.
Utilizand relatia de mai sus putem genera probabilitatea asociata fiecarei cifre.
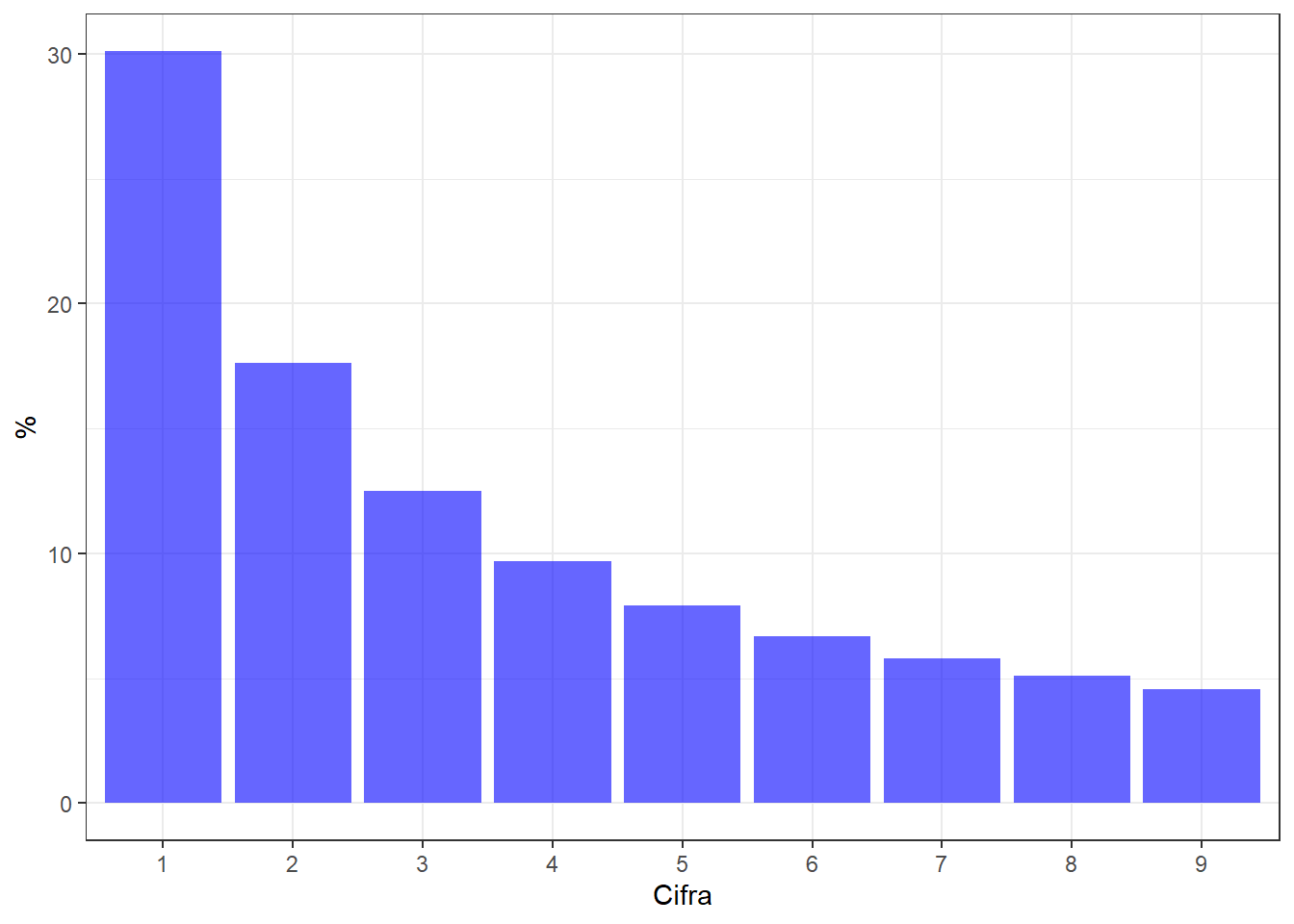
Legea este foarte simpla si se aplica unui numar mare de seturi de date. Benford a testat legea pe 20 de seturi de date care apar fie in natura fie au la baza actiunile omului. De exemplu, lungimea si suprafata raurilor din lume, numerele asociate adreselor sau rata mortalitati, toate acestea dar si multe altele seturi de date urmeaza legea lui Benford.
Acest fenomen apare din mai multe motive. O explicatie ar fi ca distributia lui Benford este o distributie secundara, adica este rezultatul unei alte distributii si anume, a distributiei numerelor din care extragem prima cifra. Cercetatorii de la Univesitatea din Essex au demonstrat [3] ca legea lui Benford apare de cele mai multe ori atunci cand sirul de date are o distributie lognormala, este unimodala si are o asimetrie pozitiva. Tot acestia mentioneaza ca nu exista o regula generala si legea lui Benford apare si in alte cazuri acoperite de urmatoarele lucrari [3], [4], [5].
In 1972, Hal Varian propune aplicarea legi in detectarea fraudelor financiare. Practic odata stabilita aplicabilitatea legii pe un tip de date abaterea unui alt set de date de acelasi tip de la legea lui Benford ar trebui investigata. Asa a ajuns legea lui Benford sa fie folosita in alegeri [6], contabilitate, cercetare si chiar intr-un film cel putin interesant numit The Accountant. Foarte important este faptul ca lege lui Benford nu te gaseste vinovat daca datele tale nu urmeaza distributia ci doar arunca un semn de indoiala asupra acestora. De multe ori dupa investigarea amanuntita a datelor s-a dovedit ca datele sunt corecte si sunt alte surse care influenteaza abaterea datelor de la legea lui Benford.
Acum despre paduri.
Discutam acum ceva vreme cu prieteni si fosti colegi aflati in productie despre datele din SILV-uri. Pentru necunoscatori SILV-urile sunt chestionare completate de ocoalele silvice si centralizate mai apoi de catre Institutul National de Statisitca. Informatiile raportate acopera activitatea silvica din Romania (plantatari, regenerari, tratamente, lemn exploatat, etc). Pe baza acestor chestionare se transmit date catre Eurostat, care centralizeaza informatiile la nivel european.
I-am intrebat cat de veridice sunt datele completate de ei si cat ma pot baza pe ele daca vreau sa le folosesc in diferite proiecte sau cercetari. Raspunsul a fost impartit, unii mi-au zis ca ei isi fac treaba corect si completeaza la virgula aceste chestionare, altii mi-au spus ca pe total bat dar compozitia speciilor nu prea, altii mi-au zis ca e foarte greu sa tii evidenta tot anul la toate lucrarile si ca le completeaza ochiometric.
Adevarul este ca nu am reusit sa trag o concluzie si am decis sa testez daca datele transmise catre Eurostat de Romania si restul Europei pentru lemnul rotund, de foc si alte produse de baza urmeaza legea lui Benford. De asemenea, am vrut sa vad daca aplicand legea lui Benford, Romania, comparativ cu alte tari europene iese din tipar.
Datele pot fi descarcate foarte usor navigand pe site-ul Eurostat sau utilizand un pachet numit eurostat care se conecteaza la baza de date a Eurostatului si iti permite accesarea datelor prin doar cateva linii de cod in R.
Daca vreti sa reproduceti analizele aveti nevoie de urmatoarele pachete si programul R instalat:
library(BenfordTests)
require(eurostat)
require(rvest)
library(knitr)
require(dplyr)
require(ggplot2)
Dupa chemarea pachetelor interogarea bazei de date se face prin functia search_eurostat(). Am cautat baze de date care au in componenta cuvantul wood.
kable(head(search_eurostat("wood")))
| title | code | type | last update of data | last table structure change | data start | data end | values |
|---|---|---|---|---|---|---|---|
| Other land: number of farms and areas by size of farm (UAA) and size of wooded area | ef_lu_ofwood | dataset | 26.03.2009 | 27.02.2020 | 1990 | 2007 | NA |
| Roundwood removals by type of wood and assortment | for_remov | dataset | 08.12.2020 | 27.11.2020 | 1988 | 2019 | NA |
| Roundwood removals under bark by type of ownership | for_owner | dataset | 08.12.2020 | 27.11.2020 | 1992 | 2019 | NA |
| Roundwood, fuelwood and other basic products | for_basic | dataset | 08.12.2020 | 27.11.2020 | 1988 | 2019 | NA |
| Industrial roundwood by assortment | for_irass | dataset | 08.12.2020 | 27.11.2020 | 1992 | 2019 | NA |
| Industrial roundwood by species | for_irspec | dataset | 08.12.2020 | 27.11.2020 | 1992 | 2019 | NA |
Cautarea a gasit 6 seturi de date dar eu sunt interesat de setul Roundwood, fuelwood and other basic products care are date din 1988 pana in 2019 si a fost acutlizata ultima data pe 08.12.2020. Folosind aceeasi functie si id-ul descarcarea bazei de date se face cu functia get_eurostat().
id <- search_eurostat("Roundwood, fuelwood and other basic products",
type = "dataset")$code[1]
dat <- get_eurostat(id, time_format = "num",type = "label")
kable(head(dat))
| prod_wd | treespec | stk_flow | unit | geo | time | values |
|---|---|---|---|---|---|---|
| Other agglomerates | Total - all species | Exports | Thousand euro | Austria | 2019 | 6168.94 |
| Other agglomerates | Total - all species | Exports | Thousand euro | Bulgaria | 2019 | 1828.48 |
| Other agglomerates | Total - all species | Exports | Thousand euro | Switzerland | 2019 | 340.07 |
| Other agglomerates | Total - all species | Exports | Thousand euro | Cyprus | 2019 | 0.00 |
| Other agglomerates | Total - all species | Exports | Thousand euro | Czechia | 2019 | 7296.77 |
| Other agglomerates | Total - all species | Exports | Thousand euro | Germany (until 1990 former territory of the FRG) | 2019 | 12761.00 |
Folosind functia de mai jos, am obtinut valorile unice primele patru coloane. Pe baza acestora am selectat valorile in mii de metri cubi care includ toate speciile si am elimninat tarile Malta, Islanda si agregarea facuta pentru cele 27 de tari europene la nivelul anului 2020 pentru ca au un numar redus de date. De asemenea denumirea Germaniei si a Europei era prea lunga (Germany (until 1990 former territory of the FRG), European Union - 28 countries (2013-2020)) si le-am redenumit.
apply(dat[c(1:4)],2,unique)
## $prod_wd
## [1] "Other agglomerates"
## [2] "Wood charcoal"
## [3] "Wood chips and particles"
## [4] "Wood chips, particles and residues"
## [5] "Wood pellets"
## [6] "Wood pellets and other agglomerates"
## [7] "Recovered wood"
## [8] "Wood residues (including wood for agglomerates)"
## [9] "Roundwood (wood in the rough)"
## [10] "Fuelwood (including wood for charcoal)"
## [11] "Industrial roundwood"
##
## $treespec
## [1] "Total - all species" "Coniferous"
## [3] "Non-coniferous" "Non-coniferous: Tropical species"
##
## $stk_flow
## [1] "Exports" "Exports to non-EU countries"
## [3] "Imports" "Imports from non-EU countries"
## [5] "Production"
##
## $unit
## [1] "Thousand euro" "Thousand units of national currency"
## [3] "Thousand tonnes" "Thousand cubic metres"
prod<-dat %>% filter(!geo %in% c("European Union - 27 countries (from 2020)","Malta","Iceland")&unit=="Thousand cubic metres")
prod<-prod[!is.na(prod$values),]
prod$geo[grep("Germany", prod$geo)]<-"Germany"
prod$geo[grep("European", prod$geo)]<-"EU"
prod_2<-prod
Analiza se va concentra pe prima cifra a fiecarei valori transmise. Legea lui Benford se aplica si celei de-a doua cifre dintr-un numar dar cu alte proportii datorita cifrei 0.
prod$first_digit<-as.numeric(substr(prod$values, 1, 1))
prod$second_digit<-as.numeric(substr(prod$values, 2, 2))
prod<-prod %>% filter(first_digit>0) %>%
group_by(geo,first_digit)%>% dplyr::summarise(n=n()) %>% mutate(prop=n/sum(n)*100)
prod$benford<-log10((prod$first_digit+1)/prod$first_digit)*100
prod$first_digit<- as.factor(prod$first_digit)
gg1<-
ggplot(data=prod,aes(first_digit, prop, fill=geo))+
geom_bar(stat="identity",show.legend = FALSE)+
geom_line(data=prod, aes(first_digit,benford, group=geo), col="red",show.legend = FALSE)+
facet_wrap(~geo)+
labs(x="Cifra",y="%")+
theme(legend.position = "none")+
theme_bw()
gg1
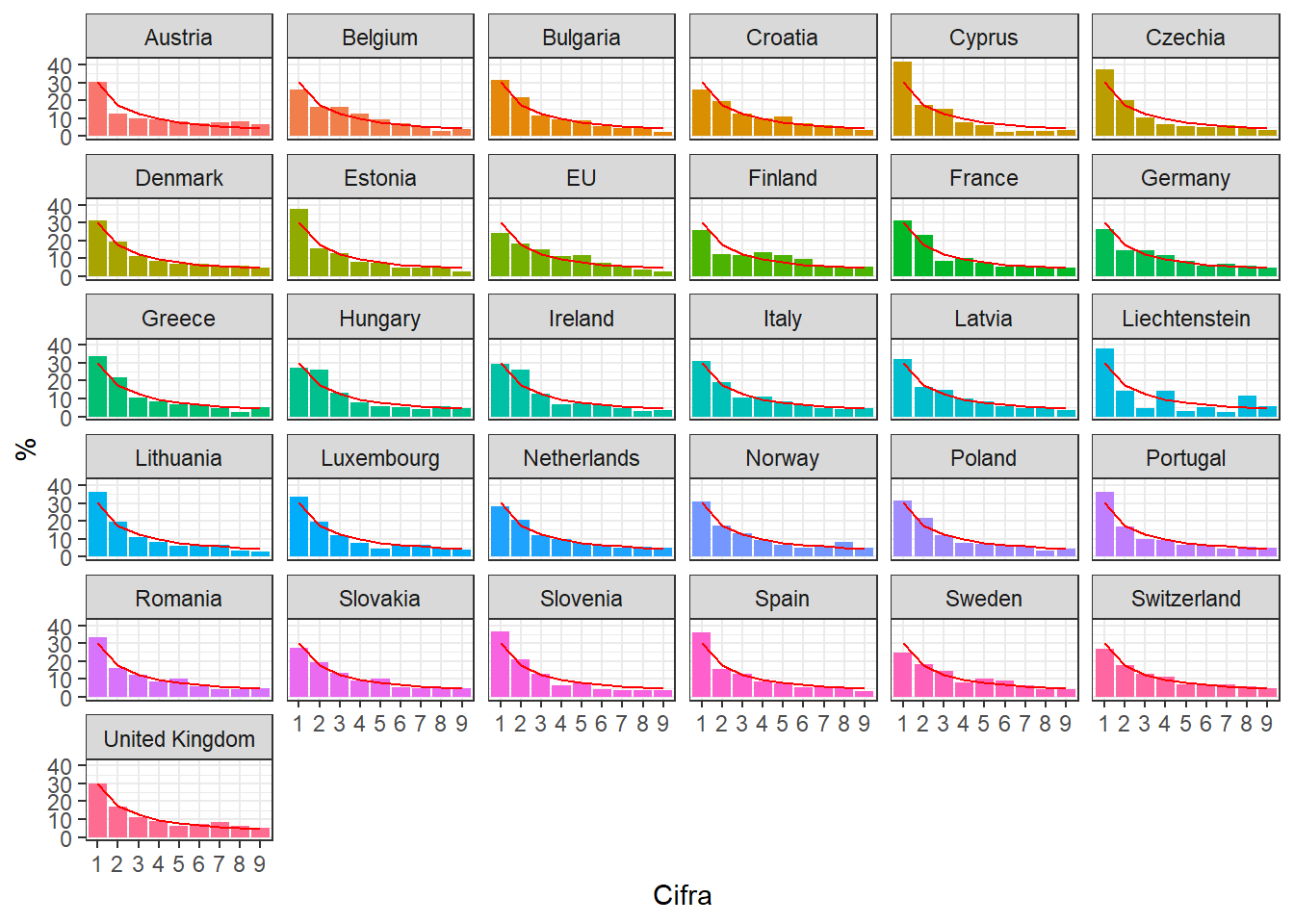 Linia rosie reprezinta distributia teoretica a lui Benford iar barele reprezinta distributia experimentala (reala) aferenta fiecarei tari.
Din graficul de mai sus se pare ca majoritatea tarilor au aceeasi distributie negativ exponentiala in care cifra 1 apare in proportie de aproximativ 30-40%.
Linia rosie reprezinta distributia teoretica a lui Benford iar barele reprezinta distributia experimentala (reala) aferenta fiecarei tari.
Din graficul de mai sus se pare ca majoritatea tarilor au aceeasi distributie negativ exponentiala in care cifra 1 apare in proportie de aproximativ 30-40%.
In R gasim un alt pachet numit BenfordTests care permite evaluarea din punct de vedere statistic a distributiei lui Benford. Testul Kogmolorov-Smirnov este deseori folosit in analize de acest gen si l-am folosit si eu pentru a determina cat de apropiata este distributia fiecarei tari de distributia legii lui Benford. Testul Kolgomorov-Smirnov calculeaza o statisitca numita D care reprezinta distanta absoluta dintre distributia teoretica si cea experimentala. Cu cat D de este mai aproape de 0 cu atat distributia tarii este mai apropiata de cea a lui Benford. De asemenea, atunci cand p-value este mai mare de 0.05 atunci setul de date urmeaza legea lui Benford, cand este sub 0.05 setul de date nu respecta legea lui Benford. Am scris o functie care va trece prin setul de date al fiecarei tari si va calcula indicatorul D precum si valoarea p.
d_test<-function(df){
df_test<-ks.benftest(df$values, digits = 1, pvalmethod = "simulate")
df_out<-data.frame(D=df_test$statistic,p_value=df_test$p.value, geo=df$geo[1])
return(df_out)
}
output<-do.call(rbind.data.frame,prod_2 %>% split(.$geo)%>% map(~d_test(.x)))
output$Semnificatie<-ifelse(output$p_value>0.05,"DA","NU")
output %>% ggplot (aes(reorder(geo,-D),D, fill=Semnificatie),)+
geom_bar(stat = "identity")+
coord_flip()+
labs(x="",y="D")+
theme_bw()
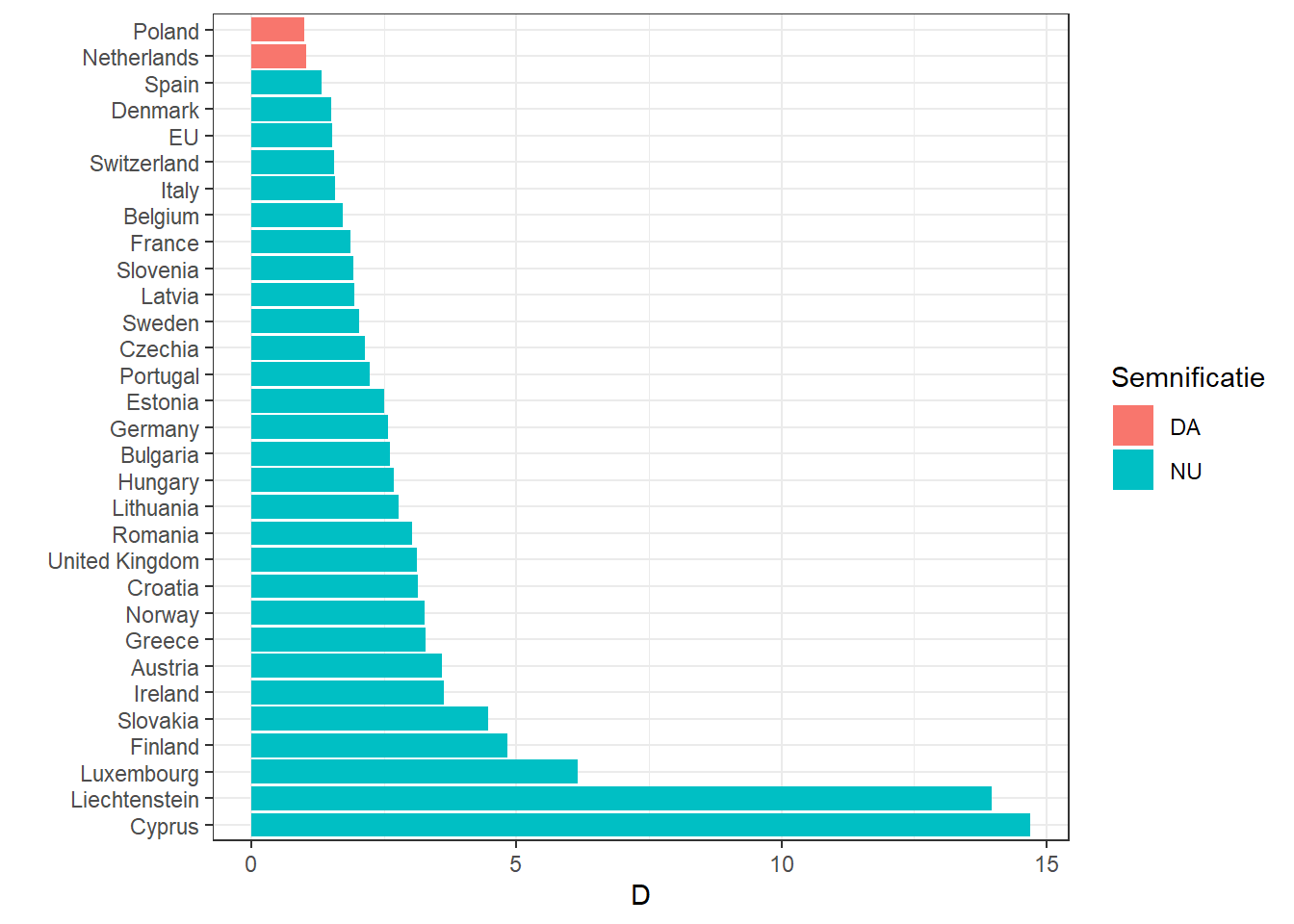 Se pare ca doar doua tari urmeaza perfect legea lui Benford. Romania se situeaza relativ bine, apropiata de media Europeana si cu o abatere de aproximativ 3.5 fata de distributia teoretica a lui Benford. Motivele pentru care aceste seturi de date nu urmeaza perfect legea lui Benford pot fi diverse. Unul dintre motive este marimea setului de date pentru fiecare tara. Ultimele trei tari nu au o activitate silvica intensa iar setul de date in cazul lor a fost redus. De asemenea, in analiza am folosit multiple seturi de date (lemn rotund, lemn de foc, lemn rotund pentru industrie) iar aceasta decizie influenteaza rezultatul. Exista insa si posibilitatea ca analiza sa fie corecta si asta sa fie adevarata abatere a datelor la nivel european de la legea lui Benford. Pentru a ne face o idee clara ar trebui aplicate si comparate cel putin inca doua teste statistice. Mai departe analiza poate continua si se poate indrepta catre cifrele din sir care nu respecta legea lui Benford. Pachetul folosit mai sus ofera o varietate de teste in acest sens. Pentru mine insa, a fost destul sa-mi fac o idee asupra validitatii datelor pe plan european si sa testez aplicabilitatea legii lui Benford pe un set de date despre silvicultura.
Se pare ca doar doua tari urmeaza perfect legea lui Benford. Romania se situeaza relativ bine, apropiata de media Europeana si cu o abatere de aproximativ 3.5 fata de distributia teoretica a lui Benford. Motivele pentru care aceste seturi de date nu urmeaza perfect legea lui Benford pot fi diverse. Unul dintre motive este marimea setului de date pentru fiecare tara. Ultimele trei tari nu au o activitate silvica intensa iar setul de date in cazul lor a fost redus. De asemenea, in analiza am folosit multiple seturi de date (lemn rotund, lemn de foc, lemn rotund pentru industrie) iar aceasta decizie influenteaza rezultatul. Exista insa si posibilitatea ca analiza sa fie corecta si asta sa fie adevarata abatere a datelor la nivel european de la legea lui Benford. Pentru a ne face o idee clara ar trebui aplicate si comparate cel putin inca doua teste statistice. Mai departe analiza poate continua si se poate indrepta catre cifrele din sir care nu respecta legea lui Benford. Pachetul folosit mai sus ofera o varietate de teste in acest sens. Pentru mine insa, a fost destul sa-mi fac o idee asupra validitatii datelor pe plan european si sa testez aplicabilitatea legii lui Benford pe un set de date despre silvicultura.
Referinte
1.Necomb, S. (1881). Note on the frequency of use of different digits in natural number. American Journal ofMathematics, 4, 39-40.
2. Benford, F. (1938). The law of anomalous numbers. Proceedings of the American philosophical society, 551-572.
3. Scott, P. D., & Fasli, M. (2001). Benford’s law: An empirical investigation and a novel explanation. Unpublished manuscript
4. Berger, A., & Hill, T. P. (2011). A basic theory of Benford’s Law. Probability Surveys, 8, 1-126.
5. Fewster, R. M. (2009). A simple explanation of Benford’s Law. The American Statistician, 63(1), 26-32.
6. Deckert, J., Myagkov, M., & Ordeshook, P. C. (2011). Benford’s Law and the detection of election fraud. Political Analysis, 19(3), 245-268.