Prins, marcat, recapturat

Cati iepuri are padurea sau cum estimezi numarul de exemplare al unei populatii? Ideal ar fi sa numaram toate exemplarele populatie dar acest lucru nu este fezabil. Zilele trecute cautand in diferite surse modalitati prin care pot estima numarul total al unei populatii cercetate, am dat peste o statistica interesanta, modelul Lincoln-Petersen [1]. Acest model este des folosit in determinarea numarului total al populatiilor de animale din salbaticie. Modelul este foarte simplu de implementat si se aplica unor populatii inchise. O populatie inchisa este o populatie care se poate deplasa pe un spatiu limitat, adica nu poate primi alti indivizi de la alta populatie iar indivizii acesteia nu pot iesi din zona populata. De asemenea acest model presupune ca rata mortalitatii si a natalitatii sunt egale. Aceste presupuneri sunt rareori indeplinite dar exista modalitati prin care se pot corecta eventualele erori rezultate din incalcarea acestor presupuneri. Metoda se mai numeste si prinde-marcheaza-recaptureaza care practic sumarizeaza metodologia aplicata.

Metodologia presupune doua etape. In prima etapa este prins un esantion de exemplare si marcat fiecare individ astfel incat marcajul sa nu se piarda. Exemplarele primului esantion sunt eliberate astfel incat sa se asigure amestecul omogen al acestora in populatie. In a doua etapa este prins un alt esantion care va fi format din exemplarele marcate in prima etapa si exemplare nemarcate. Modelul se bazeaza pe presupunerea ca proportia de indivizi marcati din totalul indivizilor prinsi in a doua etapa este egala cu proportia indivizilor prinsi in prima etapa din populatia totala. Practic numarul total al indivizilor din populatie se poate determina folosind ecuatia: $$ \frac{R}{C}=\frac{M}{N}=>N=\frac{MC}{R} $$ unde $ N $ reprezinta numarul total al indivizilor, $ M $ reprezinta numarul indivizilor capturati prima oara, $ C $ reprezinta numarul indivizilor capturati a doua oara iar $ R $ reprezinta numarul indivizilor marcati. Daca numarul de indivizi prinsi este mic atunci se prefera o formula modificata: $$ N=\frac{(M+1)(C+1)}{R+1}-1 $$

In R putem scrie un mic program care sa simuleze intreg procesul de prindere, marcare si recapturare. Sa presupunem ca noi stim care este populatia de iepuri din zona si vrem sa testam daca modelul Lincoln-Petersen functioneaza. Populatia noastra este alcatuita din 800 de iepuri care au fost deja numerotati de la 1 la 800, iar pentru a-i prinde am amplasat 10 sisteme de capturare in zone des frecventate de iepuri. Vom folosi functia sample care extrage aleatoriu un numar de elemente dintr-o multime specificata. De exemplu, functia de mai jos extrage 10 elemente aleatoriu dintr-un sir de numere de la 1 la 400, iar numerele sunt returnate mai jos 284, 336, 101, s.a.m.d. Daca rulam din nou functia vom obtine alte 10 numere diferite. Prin setarea argumentului replace=FALSE ii spunem functiei ca un numar poate fi extras doar o singura data, adica nu vom avea de mai multe ori in cele 10 numere aceeasi cifra.

require(kableExtra)
require(ggplot2)
library(plyr); library(dplyr)
require(reshape2)

sample(size = 10,x = seq(1,400,1),replace = FALSE)

##  [1] 284 336 101 111 393 133 388  98 103 214

Mai sus, argumentul size a fost specificat de noi ca fiind 10 insa acesta poate fi considerat numarul de iepuri prinsi in prima etapa. Putem scrie o alta functie sample care sa determine numarul de iepuri prinsi in prima etapa, adica litera M din functia lui Lincoln-Petersen. Stiind ca am amplasat 10 sisteme de capturare si stiind cat de performante sunt acestea numarul minim de iepuri pe care il putem avea in prima etapa este de 10, unul pentru fiecare sistem iar numarul maxim este de 800, adica intreaga populatie. Asadar functia care va determina numarul de iepuri prinsi poate fi scrisa ca:

M<-sample(size = 1,x = seq(10,800,1))
M

## [1] 293

unde size=1 pentru ca avem nevoie doar de un numar iar multimea din care va extrage este de la 10 la 800. Se pare ca am capturat 293 de iepuri deci M= 293. Avand acum marimea primului esantion putem sa vedem care iepuri au fost prinsi.

k<-sample(size = M,x = seq(1,800,1),replace = FALSE)
k

##   [1] 284 101 623 645 400  98 103 726 602 326  79 270 382 184 574   4 661 552
##  [19] 212 195 511 479 605 634 578 510 687 424 379 108 131 343  41 627 740 298
##  [37] 258 629 790 182 305 358 696 307 760 221 736 561 313 136 145 123 234 608
##  [55] 495 534 297 208 770 569 522 248 365 665 643 595 434 218 727 508 276 169
##  [73]  71 573 791 485 667 460  60 449 548  19 649 638 670 319 116 750 102 214
##  [91] 390 597 709 160  77 529 126 262 442 642 181 163 474 228 712 646 265 427
## [109] 719 249 745  40 541 497 796 450 600 716 363 478 403 375 335 598 142 444
## [127] 680 659 728 457 188 432 488 538 690 215 540 613 669 296 328 147  84  83
## [145] 250 705 281 431  30  10 666 441 753 345 592 585  12 293 303 677 338 350
## [163] 673 107 543 518 785  43 189 171  39 216 291  58 395 787 456  22 170 588
## [181]  63 622 417 732  70  59 484 203 227 243 413 577 542 476 617 766 405 397
## [199] 501 429 205 475 104 210 471  66  88 759 309 676 294 421 707 430 512 361
## [217] 714 480  15 486 254 491 654 178 428 637 194 738 378 589 155 166 207 468
## [235] 105 482 280 440 389 499 251 231 590 463 100 683 141 772 553  36 730 362
## [253]  86 138 344 211 461 544 762 792 746 371 380  97  49 469 260 599 174 713
## [271] 662 183 347  74 591 581 118 271 695 357 252 570 778 459  61 179 272  76
## [289]  87 224 678 668 164

Din cei 800 de iepuri am prin iepurele 284, 101 pana la iepurele 164. I-am marcat pe toti si le dam drumul inapoi in libertate. Mergem la etapa a doua. Amplasam din nou cele 10 sisteme de capturare si prindem iepurii ruland din nou aceasi functie care determina cati iepuri am prins. Rezultatul este 151 de iepuri, deci C=151

## [1] 151

Hai sa vedem cati dintre cei 151 sunt marcati. Rulam din nou functia sample cu argumentul size=C

q<-sample(size = C,x = seq(1,800,1))
q

##   [1] 142  51 720 730 220 664 605 587 352 216 770  86  75  38 615 778 465  40
##  [19] 286 257 724 506  12 771 393  14 653 704 148 618 528 592  62 480 354 500
##  [37] 635 572 537  36 744 166 649 723 145 756 677 570 106 451 757  13 735 579
##  [55] 433 586  56 363 504  91 628 546 675 621 726 567 234 255 535 154 439 399
##  [73]  46 471  90 124 472 517 743 580 377 323  74   7 554 346 311 644 737 544
##  [91] 449 796 432 748 755   3  18 453 458 647 249 404 396 324 419 390 376 543
## [109] 355 232 665 176 762 412  76 512  92 356 520 590 146 699 341  21  47 267
## [127] 799  71  63 244 574 617 110 253 760 468  37 738 758  10 455 753  77 610
## [145] 338 129 485 656 794 525 175

Folosind functia intersect comparam cele doua seturi de numere si identificam cate cifre se regasesc in cele doua seturi, respectiv cati iepuri marcati au fost prinsi in a doua etapa.

R<-length(intersect(k,q))
R

## [1] 46

Doar 46 de iepruri marcati au fost identificati in a doua etapa, deci R=46.

Avand toate elementele ecuatiei putem inlocui si determina N, adica numarul total al populatiei. Noi stim ca este 800 dar vrem sa vedem cat de bine functioneaza modelul Lincoln-Petersen. Folosind formula pentru un numar redus, N este egal cu 950.

N<-((M+1)*(C+1)/(R+1))-1
round(N)

## [1] 950

Nu este departe de 800. Se poate calcula eroarea modelului pentru a determina intervalul de incredere al acestei statistici. Varianta $ (s^2) $, deviatia standard $ (s) $ si intervalul de incredere de 95% se pot calcula cu urmatoarele formule:

$$ s^2=\frac{(M+1)(C+1)(M-R)(C-R)}{(R+1)^2(R+2)} $$

varN<-((M+1)*(C+1)*(M-R)*(C-R))/(((R+1)^2)*(R+2))
varN

## [1] 10930.5

$$ s=\sqrt(s^2) $$

s<-sqrt(varN)
s

## [1] 104.5491

$$ N\pm1.965*s $$

round(N- 1.965* sqrt(varN))

## [1] 744

round(N+ 1.965* sqrt(varN))

## [1] 1155

Asadar N este 950 cu un interval de incredere de 95% cuprins intre 744 si 1155. Numarul real al populatiei este inclus in intervalul de incredere al estimarii noastre deci modelul Lincoln-Petersen reuseste sa estimeze cu succes numarul total al populatiei de iepuri. Intrebarea este, ce se intampla daca este repetat intreg experimentul, vom ajunge la acelasi rezultat? Putem afla foarte usor introducand liniile de cod de mai sus intr-un for loop care sa repete intreg procesul de prindere, marcare si recapturare de 100 de ori.

out<- data.frame(matrix(nrow = 100,ncol=4,))
names(out)<-c("M","C","R","N")
for (i in 1:100){
  M<-sample(size = 1,x = seq(10,800,1)) 
  k<-sample(size = M,x = seq(1,800,1),replace = FALSE)
  C<-sample(size = 1,x = seq(10,800,1))
  q<-sample(size = C,x = seq(1,800,1))
  R<-length(intersect(k,q))
  N<-((M+1)*(C+1)/(R+1))-1
  out$M[i]<-M
  out$C[i]<-C
  out$R[i]<-R
  out$N[i]<-round(N)
}

mu <-  out %>% melt()%>%ddply( "variable", summarise, grp.mean=mean(value))
  out %>% melt()%>%
   ggplot(aes(x=value, fill=variable))+
   geom_histogram()+
   labs(y= "Frecventa",x="Valoare", fill="Parametru")+
   geom_vline(data=mu, aes(xintercept=grp.mean), color="black", size=1.3,
             linetype="dashed")+
    facet_wrap(~variable, scales= "free")

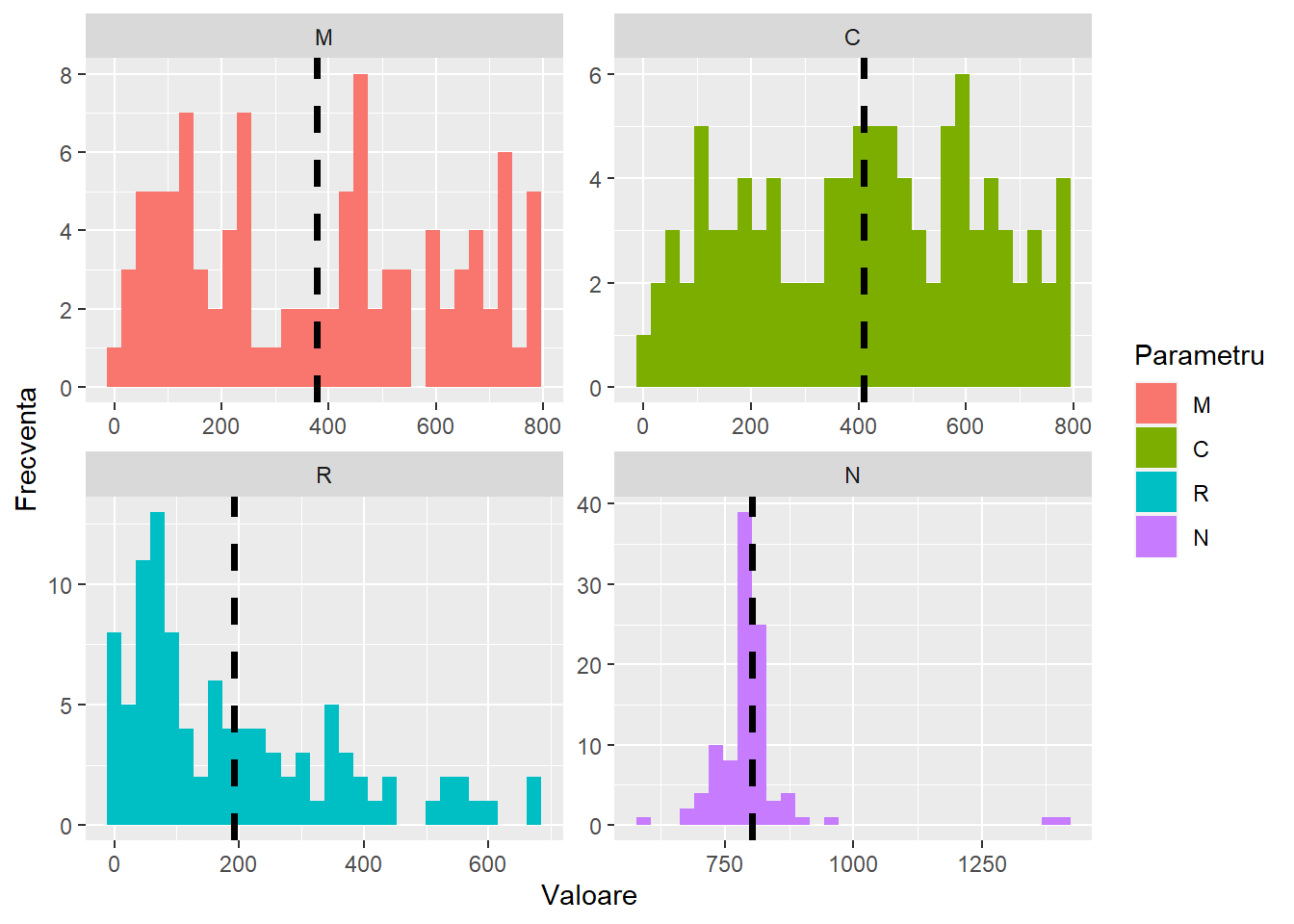Distributia celor 100 de simulari demonstreaza ca majoritatea estimarilor N se situeaza in jurul cifrei 800, linia neagra punctata indica media celor 100 de simulari pentru fiecare parametru.

Media numarului de iepuri (N) este 802 cu un interval de incredere de 95% cuprins intre 610 si 993.

round(mean(out$N))

## [1] 802

round(mean(out$N)- 1.965* sqrt(var(out$N)))

## [1] 610

round(mean(out$N)+ 1.965* sqrt(var(out$N)))

## [1] 993

In R exista mai multe pachete destinate acestui fel de analize. Unul dintre acestea este numit marker care permite estimare numarului de indivizi si pentru populatii deschise.

Spor la prins, marcat si recapturat!

Referinte

1. Nichols, J. D. (1992). Capture-recapture models. BioScience, 42(2), 94-102.